引言
这篇博文作为大二数据结构与算法课程自己觉得有意思的算法题的整理记录,不定时更新。
一、用List类实现一元多项式的表示与相加
1、链表的实现
结构体Node作为链表结点,包含指针next与两个整型元素:value系数和index指数。
List类包含头指针,头指针指向头结点,头结点默认元素为0。(加上头结点真的可以简化很多操作,insert、delete等操作不需将首尾单独实现)各个结点根据指数由低到高排列。
List类的成员函数包括构造函数、析构函数、插入元素、删除元素、查找元素、两个链表的相加。
struct Node{
Node* next;
int value,index;
Node(int val=0,int ind=0):value(val),index(ind),next(NULL){}
};
class List{
public:
Node* head;
List() {
head = new Node();
head->next=NULL;
}
~List(){
while(head != NULL){
Node *temp=head;
head=head->next;
delete temp;
}
}
void clear(){
while(head != NULL){
Node *temp=head;
head=head->next;
delete temp;
}
head = new Node();
head->next=NULL;
}
void Insert(Node* n);
void DeleteElement(int k);
Node* SearchkthNode(int k);
void MergeList(List &List1, List &List2);
};
2、具体函数实现
(1)链表元素插入:
比较新加入结点n的指数,确定该结点插入的位置,进行插入。
void List::Insert(Node* n){
if(n->value==0)return;
Node *temp=head;
while(temp->next != NULL){
if(temp->next->index >= n->index) break;
temp=temp->next;
}
if(temp->next==NULL || temp->next->index > n->index) {
Node *p= temp->next;
temp->next=n;
n->next=p;
}
else {
temp->next->value += n->value;
delete n;
}
return;
}
(2)链表元素删除:
找到第k个结点,将其删除。(第一个元素定义为结点1,以此类推)
void List::DeleteElement(int k){
if(k<=0)return;
Node *temp=head;
for(int i=0;i<k-1 && temp != NULL;i++){
temp=temp->next;
}
if(temp == NULL || temp->next==NULL)return;
Node *p=temp->next;
temp->next=p->next;
delete p;
return;
}
(3)链表元素查找:
查找第k个结点,返回该结点的指针,若该结点不存在,返回NULL。
Node* List::SearchkthNode(int k){
if(k<=0)return NULL;
Node *temp=head;
for(int i=0;i<k && temp != NULL;i++){
temp=temp->next;
}
return temp;
}
(4)两个链表进行相加:
两个链表list1、list2作为参数传入,进行成员函数操作的链表作为相加的结果。
首先,如果该链表不为空,则先将链表清空,以便插入操作。将p1p2分别指向两个源链表的第一个元素(注意不是头结点),比较两个结点的指数大小,将较小的结点插入新链表尾部;若两个结点指数相等,则将两个结点的系数相加后进行插入。每进行一次插入操作,p1p2向后移一位,直到指向NULL。
进行结点操作时注意我们的链表是有头结点的,不需要对头结点进行操作。
void List::MergeList(List &list1, List &list2){
if(head != list1.head && head != list2.head){
this->clear();
}
Node *newhead,*p1=list1.head->next,*p2=list2.head->next;
newhead = new Node();
Node *t=newhead;
while(p1 != NULL && p2 != NULL){
if(p1->index>p2->index){
Node *newone=new Node(p2->value,p2->index);
t->next=newone;
t=t->next;
p2=p2->next;
}
else if(p1->index<p2->index){
Node *newone=new Node(p1->value,p1->index);
t->next=newone;
t=t->next;
p1=p1->next;
}
else {
if(p1->value+p2->value!=0){
Node *newone=new Node(p1->value+p2->value,p1->index);
t->next=newone;
t=t->next;
}
p1=p1->next;
p2=p2->next;
}
}
while(p2!=NULL){
Node *newone=new Node(p2->value,p2->index);
t->next=newone;
t=t->next;
p2=p2->next;
}
while(p1!=NULL){
Node *newone=new Node(p1->value,p1->index);
t->next=newone;
t=t->next;
p1=p1->next;
}
head=newhead;
return;
}
3、main测试函数
main函数利用srand((int)time(NULL)); 与rand()%int生成随机数进行测试,注意包含头文件#include<windows.h>、#include<time.h>。
int main(){
List list1,list2;
Node *n1,*n2;
srand((int)time(NULL));
for(int i=0;i<10;i++){
n1=new Node(rand()%20,rand()%20);
list1.Insert(n1);
}
cout<<"list1=";
Node *t=list1.head->next;
while(t!=NULL){
cout<<t->value<<"x^"<<t->index;
t=t->next;
if(t!=NULL)cout<<" + ";
}
cout<<endl;
for(int i=0;i<10;i++){
n1=new Node(rand()%20,i);
list2.Insert(n1);
}
cout<<"list2=";
t=list2.head->next;
while(t!=NULL){
cout<<t->value<<"x^"<<t->index;
t=t->next;
if(t!=NULL)cout<<" + ";
}
cout<<endl;
List n;
n.MergeList(list1,list2);
t=n.head->next;
cout<<"n=";
while(t!=NULL){
cout<<t->value<<"x^"<<t->index;
t=t->next;
if(t!=NULL)cout<<" + ";
}
}
——2019-09-06
二、链表排序
给定一个链表和一个值X,操作使得节点值小于X的节点都在大于等于X的节点的前面,并保持每个分区节点的相对顺序不变。
-
输入样例 3
6->5->4->3->2->1->5->0 -
输出样例 2->1->0->6->5->4->3->5
1、链表结构
struct linkNode {
int val;
linkNode *next;
linkNode(){
val=0;
next=NULL;
}
linkNode(int x) : val(x), next(NULL) {}
~linkNode(){}
};
linkNode* partList(linkNode *head, int x);
2、排序函数的实现
linkNode* partList(linkNode *head, int x)函数用于创造一个完成排序的链表,返回其头指针。
排序中最重要的部分是保持其相对顺序不变,实际上可以简单理解成将链表分割成两个子链表,每个子链表中元素的相对顺序与源链表相同,只要在最后将两个子链表连接,就可以得到排序后的链表。
源链表:6->5->4->3->2->1->5->0 (x=3)
子链表一:2->1->0
子链表二:6->5->4->3->5
重新连接:2->1->0->6->5->4->3->5
linkNode* partList(linkNode *head, int x){
linkNode *p=head;
linkNode *p1=new linkNode(0); //子链表一,为其创建头结点
linkNode *p2=new linkNode(0);//子链表二,为其创建头结点
linkNode *h1=p1,*h2=p2; //需要记录子链表的头结点,且每次都在尾结点插入新元素
while(p!=NULL){ //遍历整个链表
if(p->val < x){
p1->next=new linkNode(p->val); //若结点数值比x小,给子链表一插入元素
p1=p1->next;
}
else {
p2->next=new linkNode(p->val);//若结点数值大于等于x,给子链表二插入元素
p2=p2->next;
}
p=p->next;
}
p1->next=h2->next;
return h1->next; //注意子链表一、子链表二都有头结点,返回时需要跳过
}
3、main测试函数
int main(){
linkNode *head=NULL;
srand((int)time(NULL));
for(int i=0;i<10;i++){
linkNode *n1=new linkNode(rand()%20);
n1->next=head;
head=n1;
}
linkNode *head1=partList(head,10);
while(head!=NULL){
cout<<head->val<<endl;
head=head->next;
}
cout<<endl;
while(head1!=NULL){
cout<<head1->val<<endl;
head1=head1->next;
}
}
——2019-09-12
三、输入输出受限的双向队列
1、题目信息
若以1234作为双端队列的输入序列,分别求出满足下列条件的输出序列:
(1)能由输入受限的双端队列得到,但是不能由输出受限的双端队列得到的输出序列;
(2)能由输出受限的双端队列得到,但是不能由输入受限的双端队列得到的输出序列;
(3)既不能由输入受限的双端队列得到,也不能由输出受限的双端队列得到的输出序列。
2、基本思路
由于不想手动枚举,故想到了写一个程序遍历显示所有的情况,再比较各个情况的不同部分。基本思路是先构造一个输入输出不受限的双端链表,将1、2、3、4按顺序输入,将每一次输出依次计入一个4元素的数组中,当数组满了之后就把数组打印出来,就能得到当前情况所对应的全排列。当需要输入/输出受限时,将对应的代码注释掉即可。
为了得到不受限的所有遍历,可以利用函数调用得到所有的分支,每一次的函数调用都有队首输入、队尾输入、队首输出、队尾输出四个子调用;而当用于记录的数组满了,就打印出数组,逻辑流程图如下:
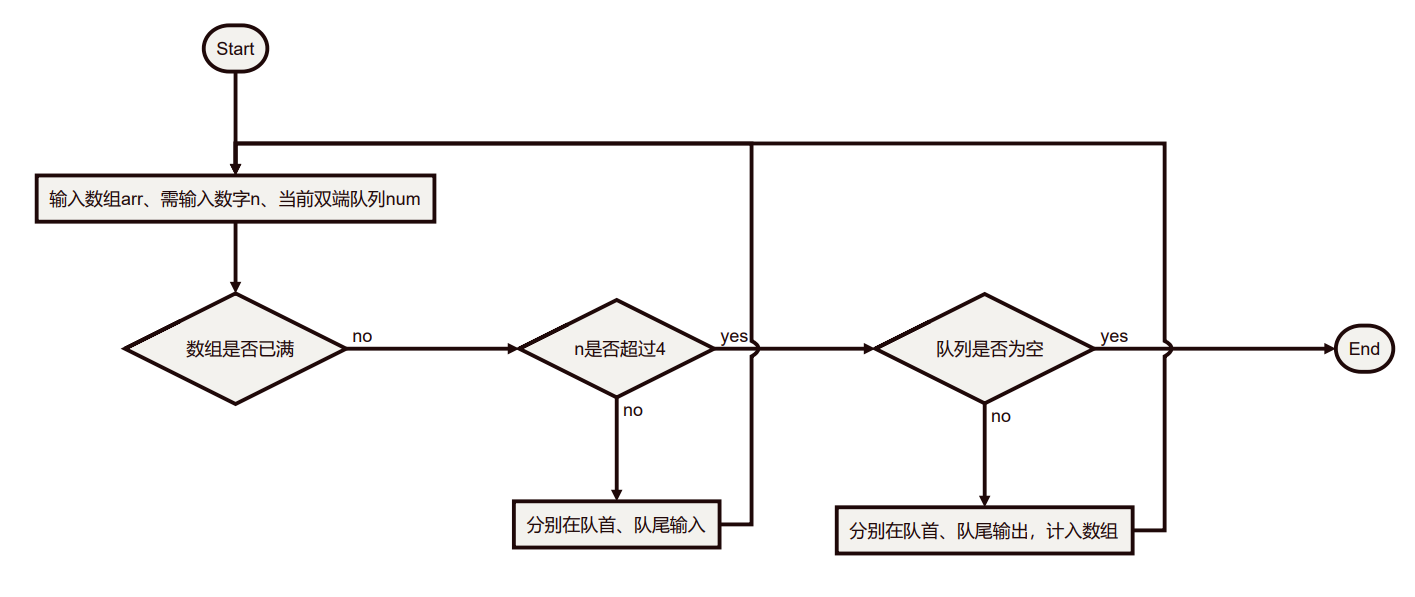
最后我们得到的函数为void fun(int *arr,int n,deque<int> num),但首先我们看看main函数:
#include<iostream>
#include <deque>
using namespace std;
int arr0[4][24];
int main(){
deque<int> num;
int arr[4]={0,0,0,0};
for(int i=0;i<4;i++){
for(int j=0;j<24;j++){
arr0[i][j]=0;
}
}
fun(arr,1,num);
for(int i=0;i<24;i++){
cout<<arr0[0][i]<<arr0[1][i]<<arr0[2][i]<<arr0[3][i]<<endl;
}
}
我们定义了一个全局变量int arr0[4][24],这是为了储存所得到的所有不同序列,由于1234的全排列有$4!=24$种,则二维数组大小为$24\times4$,若该次遍历所得到的排列与二维数组中排列不同,则存入该数组,最后再将整个数组输出。
最后是函数的实现:
void fun(int *arr,int n,deque<int> num){
int arr1[4],arr2[4],arr3[4],arr4[4];
int i=0;
for(;i<4;i++){
arr1[i]=arr[i];
arr2[i]=arr[i];
arr3[i]=arr[i];
arr4[i]=arr[i];
}
//数组创建
if(arr[3] != 0){
int diff=1;
for(int i=0;i<24;i++){
if(arr0[0][i]==arr[0] && arr0[1][i]==arr[1] && arr0[2][i]==arr[2] && arr0[3][i]==arr[3] ){
diff=0;
break;
}
}
int i=0;
for(;i<24;i++){
if(arr0[0][i]==0)break;
}
if(diff){
arr0[0][i]=arr[0];
arr0[1][i]=arr[1];
arr0[2][i]=arr[2];
arr0[3][i]=arr[3];
}
return;
}
//数组已满时,判断是否与已得排列重复,若不重复,写入二维数组中
if(n<5){
num.push_front(n);
fun(arr1,n+1,num);
num.pop_front();
}
//队首输入
if(n<5){
num.push_back(n);
fun(arr2,n+1,num);
num.pop_back();
}
//队尾输入
if(!num.empty()){
int i=0;
for(;i<4;i++){
if(arr3[i]==0)break;
}
arr3[i]=num.front();
num.pop_front();
fun(arr3,n,num);
num.push_front(arr3[i]);
}
//队首输出
if(!num.empty()){
int i=0;
for(;i<4;i++){
if(arr4[i]==0)break;
}
arr4[i]=num.back();
num.pop_back();
fun(arr4,n,num);
num.push_back(arr4[i]);
}
//队尾输出
return;
}
第一步首先创建了四个新数组,这是因为函数调用数组是以指针的形式,并没有创建新的数组,所以我们需要手动创建;同时在对队列进行输入输出时,进行每一次输入输出、调用子函数后应将队列复原至原来的情况,以保证对每一个函数的调用都是只针对一种情况。
3、运行结果
执行输入输出的双端队列,得到的是24个全排列:
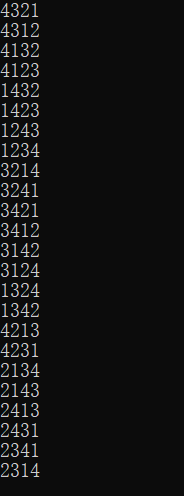
将其中一个输入注释掉,即输入受限,得到的结果少了4231、4213:
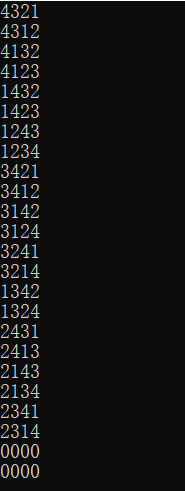
将其中一个输出注释掉,即输出受限,得到的结果少了4132、4231:
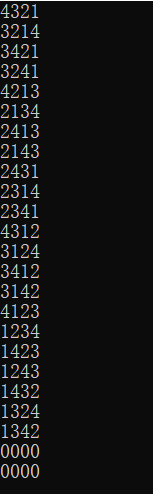
那我们得到的答案为:
-
能由输入受限的双端队列得到,但是不能由输出受限的双端队列得到的输出序列:
4132 -
能由输出受限的双端队列得到,但是不能由输入受限的双端队列得到的输出序列:
4213 -
既不能由输入受限的双端队列得到,也不能由输出受限的双端队列得到的输出序列:
4231
4、Todo
- 将固定输出改为由用户输入n,生成n个数字生成的序列。
- 输出得到的排列数顺序不固定,将输出按照一定的顺序排列再输出。
——2019-09-19
四、吃豆人
有N个级别互不相同的吃豆人在一条街道的不同位置上向左或向右移动,两个吃豆人碰面时级别高的能够吃掉级别低的,吃豆人移动的速度相同,求问足够长时间过后能够存活多少个吃豆人。
-
输入格式: 第一行N代表吃豆人的数量,N在1到99999之间。 随后N行,每行2个数A,B为从左到右排列的N个吃豆人的级别和吃豆人移动的方向,A在1到99999之间,B为0表示向左,1表示向右。
-
输入 5 4 0 3 1 2 0 1 0 5 0
-
输出 2
1、算法思路
这道题的思路比较难,我们首先考虑两个吃豆人的情况:由于速度相同,那么←←、→→、←→的情况都不会相遇,只有在→←才可能相遇。
而在→←相遇时,等级高的会吃掉等级低的,若剩下←,这个吃豆人将不会再被吃掉(假设新的吃豆人从右边出现);若剩下→,那接下来出现的吃豆人将有可能再次构成→←进行操作。
根据这个思路,我们可以用栈结构完成这道题,将吃豆人从左到右依次压栈,当出现→←的情况时,将需要入栈的吃豆人与栈顶的吃豆人比较,当等级低时弹出,直到栈顶的吃豆人比当前吃豆人等级高,则比较下一吃豆人(或者栈空或出现←的吃豆人,则将当前吃豆人入栈);直到所有吃豆人都入栈之后,统计当前栈内吃豆人的个数,则是最终结果。
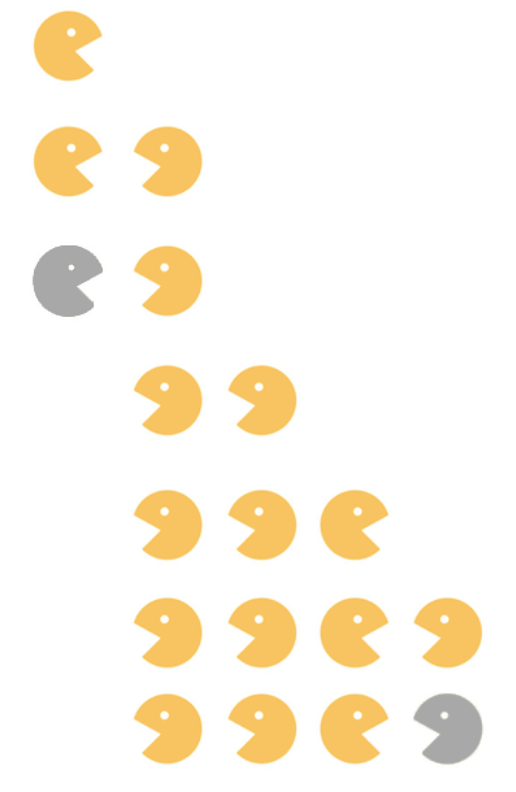
2、代码实现
#include <iostream>
#include <stack>
using namespace std;
struct pa{
int dec;
int lev;
}; //吃豆人结构体
int main()
{
int n;
cin >> n;
stack<pa> sta;
pa a;
cin>>a.lev>>a.dec;
sta.push(a); //将第一个吃豆人入栈,防止下面的判断出现栈空
for(int i=1;i<n;i++){ //从第二个吃豆人开始
pa p;
cin>>p.lev>>p.dec;
if(p.dec==0 && sta.top().dec==1){ //→←的情况
while(!sta.empty() && sta.top().dec==1 && sta.top().lev<p.lev ){
sta.pop();
}//循环直到→←的情况结束
if(sta.empty() || sta.top().dec==0)
sta.push(p); //若结束后当前的吃豆人没被栈顶的吃掉,入栈
}
else sta.push(p); //其他情况,直接压栈即可
}
int num=0;
while(!sta.empty()){
sta.pop();
num++;
}
cout << num;
}
——2019-10-07
五、括号匹配
给定一个字符串,确认该字符串中的括号是否合法,如果合法输出True,不合法输出False。 判定规则,只有形如(),[],{}这样的格式才算合法,可以嵌套括号。
- 例: ({}[])(){} True
({}[])( False
没什么难度,直接栈实现,若右括号无法匹配栈中的左括号/最后栈不空,则输出False。
代码如下:
#include<iostream>
#include<string>
using namespace std;
int main(){
string x;
cin>>x;
int arr[x.size()]; //数组做栈
int n=0; //n为元素个数,n-1指向栈顶
for(int i=0;i<x.size();i++){
switch(x[i]){
case '(':{
arr[n]=0;
n++;
break;
}
case '[':{
arr[n]=1;
n++;
break;
}
case '{':{
arr[n]=2;
n++;
break;
}
case ')':{
if(arr[n-1]==0){
n--;
}
else{
cout<<"False";
return 0;
}
break;
}
case ']':{
if(arr[n-1]==1){
n--;
}
else{
cout<<"False";
return 0;
}
break;
}
case '}':{
if(arr[n-1]==2){
n--;
}
else{
cout<<"False";
return 0;
}
break;
}
}
}
if(n==0)cout<<"True";
else cout<<"False";
}
这道题写出来主要是为了下一道题服务。
——2019-10-09
六、最长括号子串匹配
给定一个只包含小括号的字符串,求出其中最长的有效的括号的子串的长度。
-
输入 )()()(
-
输出 4
-
输入 (()
-
输出 2
1、算法思路
这种有效括号的题目很容易想到使用栈stack来处理,但是这题的难点是需要找到一个明晰的思路,不然很容易逻辑混乱。解决思路为使用一个变量start来记录最初有效字串的起始下标,这里比较值得注意的是栈中保存的不是括号字符而是括号的位置的值,这样做的目的是为了后面计算长度:
思路如下:
-
需有一个变量start记录有效括号子串的起始下标,max_len表示最长有效括号子串长度,初始值均为0
-
遍历给字符串中的所有字符 1.需有一个变量start记录有效括号子串的起始下标,max_len表示最长有效括号子串长度,初始值均为0
2.遍历给字符串中的所有字符
2.1若当前字符s[index]为左括号'(',将当前字符下标index入栈(下标稍后有其他用处),处理下一字符
2.2若当前字符s[index]为右括号')',判断当前栈是否为空
2.2.1若栈为空,则start = index + 1,处理下一字符(当前字符右括号下标不入栈)
2.2.2若栈不为空,则出栈(由于仅左括号入栈,则出栈元素对应的字符一定为左括号,可与当前字符右括号配对),判断栈是否为空
2.2.2.1若栈为空,则max_len= max(max_len, index-start+1)
2.2.2.2若栈不为空,则max_len= max(max_len, index-栈顶元素值)
2、代码实现
#include<iostream>
#include<string>
#include <stack>
using namespace std;
int Max(int a,int b){
return a>b?a:b;
}
int main(){
string str;
cin>>str;
int count=str.size(),max=0,start=0;
stack<int> num;
for(int i=0;i<count;i++){
if(str[i]=='(')
num.push(i);
else {
if(num.empty()){
start=i+1;
}
else {
num.pop();
if(num.empty()){
max=Max(max,i-start+1);
}
else max=Max(max,num.top()-start);
}
}
}
cout<<max;
}
——2019-10-12
七、坐缆车
1、问题描述
M山上设置了n个只下山不上山的缆车点1,2…n。游客可以从山上的某一点上缆车,并从其下方任意点下缆车。缆车点i到缆车点j之间的费用为r(i,j),1<=i<=j<=n。试计算从山顶1到山脚n坐缆车所需的最少费用。
输入格式:
第一行一个正整数n,表示有n个缆车点,接下来n-1行是一个半矩阵,当前行表示当前点按顺序到其下方点的费用r(i,j),从点1开始。
输出格式:
一个整数,表示最小费用
2、算法思路
本题就是一个简单的Dijkstra算法实现,给定n个缆车点和费用,图的结构和信息即得出,利用邻接矩阵存储,并进行Dijkstra运算得出最小费用即可。
3、代码实现
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int n;
int main(){
cin>>n;
int Mat[n][n];
for(int i=0;i<n;i++){
for(int j=1+i;j<n;j++){
cin>>Mat[i][j];
}
}
int visit[n],path[n];
visit[0]=0;
for(int i=1;i<n;i++){
visit[i]=Mat[0][i];
}
for(int i=1;i<n;i++){
int min=visit[i],min_ind=i;
for(int j=i;j<n;j++){
if(min>visit[j]){
min=visit[j],min_ind=j;
}
}//找最小值
for(int k=min_ind+1;k<n;k++){
int temp=visit[min_ind]+Mat[min_ind][k];
visit[k]=visit[k]<temp?visit[k]:temp;
}//最短路径
}
cout<<visit[n-1];
}
八、一笔画
1、问题描述
给定一个无向图,包含n 个顶点(编号1~n),m条边,求最少用多少笔可以画出图中所有的边,一条边不会被描绘多次。
输入格式:
第一行2个数n,m,接下来m行,每行两个数a,b表示a,b两点之间有一条边相连。
输出格式:
一个数,表示多少笔。
2、算法思路
一笔画问题只需要判断图的各个结点的度的奇偶性即可,画的笔数为奇数点个数/2。
但是上面只是针对一个连通图得到的解题方法,当图中有多个连通分支时,需要根据每个连通分支判断。
3、代码实现
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int n,m;
int main(){
cin>>n>>m;
int count[n];
for(int i=0;i<n;i++){
count[i]=0;
}
for(int i=0;i<m;i++){
int t1,t2;
cin>>t1>>t2;
count[t1-1]++;
count[t2-1]++;
}
int k=0;
for(int i=0;i<n;i++){
if(count[i]%2==1){
k++;
}
}//k为奇数点个数
if(k==0)k=2;//当没有奇数点,只需一笔
cout<<k/2;
}
代码只能得出连通图的一笔画判断,多个连通分支的判断尚未实现。
九、食物链
十、赛马问题
1、问题描述
A与B之间将进行一场赛马比赛,C为裁判。A与B分别拥有n匹马,这2n匹马中每匹马拥有的能力值都不相同。比赛前,参赛的两人先决定自己的马的出场顺序;比赛时,A的第一匹马将对战B的第一匹马,A的第二匹马将对战B的第二匹马,以此类推。在每一轮的比赛当中,能力值较高的马将获得胜利,并记其拥有者加1分。进行过n轮比赛之后,得分较高的人将获得最终的胜利,并赢得所有的马。当然,可能存在平局的情况,此时算作裁判C胜利,并获得所有的马。
问:给定每一匹马的能力值,裁判C能否通过重新调整马匹参赛顺序而获得胜利?
输入:
第一行输入一个整数n,1 <= n <= 100。
第二行输入n个整数,代表选手A所有马匹的能力值。
第二行输入n个整数,代表选手B所有马匹的能力值。
输出:
如果可以平局的话,则输出“YES”,否则输出“NO”。
2、算法思路
裁判C胜利的条件为AB平局,那么,我们可以先将AB的马排序,让A能力值最高的一半与B能力值最低的一半比赛,反之让B能力值最高的一半与A能力值最低的一半比赛,确保A、B均有一半胜出。
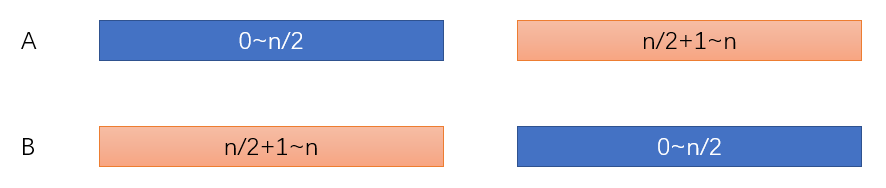
而且,在这两组比较中,我们也要确保将A、B的马按顺序比较,例如A:1,2,3,4;B:3,4,5,6;依次比较1-3、2-4、3-5、4-6,才能确保B获得所有胜利。
【不能只比较A、B组中最好、最差的马,比如上述例子会出现判断出错】
3、代码实现
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
int main() {
int n;
cin>>n;
int A[n],B[n];
for(int i=0;i<n;i++){
cin>>A[i];
}
for(int i=0;i<n;i++){
cin>>B[i];
}
for(int i=0;i<n-1;i++){
for(int j=i+1;j<n;j++){
if(A[i]>A[j]){
int temp=A[i];
A[i]=A[j];
A[j]=temp;
}
if(B[i]>B[j]){
int temp=B[i];
B[i]=B[j];
B[j]=temp;
}
}
}//对AB进行排序
int yes=1;
int mid1=n/2,mid2=mid1+1;//分成两组
for(int i=0;i<mid1;i++){
if(A[i]>B[i+mid1]){
yes=0;
}
if(B[i]>A[i+mid1]){
yes=0;
}
}
if(yes)cout<<"YES";
else cout<<"NO";
return 0;
}
十一、接雨水问题
1、问题描述
输入N个非负整数,可以表示成一个若干个方块堆积的图,图中每一列的宽度均为1,高度为输入的数字,请计算在下雨时,该图能容纳多少面积的雨水。例如:输入[0,1,0,2,1,0,1,3,2,1,2,1],如下图所示,则输出为6。

输入描述:
输入为两行,第一行为N,代表非负整数的个数,第二行为N个非负整数。
2、算法思路
算法从第一层开始计数,将每层积累的雨水数累加起来。
引入两个变量l、r,表示读取到的最邻近的两堵墙的位置;从左到右依次读取,当读取到新的墙时,更新l、r,并通过r-l得到两堵墙之间的雨水数,将其累加得到最终结果。
3、代码实现
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
int main() {
int n,h=0;
cin>>n;
int A[n];
for(int i=0;i<n;i++){
cin>>A[i];
if(h<A[i])h=A[i];//得到最高高度
}
int x=0;
for(int i=0;i<h;i++){
int l=-1,r=-1;//初始化l、r
for(int j=0;j<n;j++){
if((A[j]>=i+1)){
l=r;
r=j;//更新
if(r>=0 && l>=0){
x+=(r-l-1);//累加
}
}
}
}
cout<<x;
return 0;
}
十二、单调上升序列
1、问题描述
给定一长度为n的数列,请在不改变原数列顺序的前提下,从中随机的取出一定数量的整数,并使这些整数构成单调上升序列。 输出这类单调上升序列的最大长度。
输入格式:
第一行,一正整数n,表示数列的长度 第二行,n个数,表示数列
输出格式:
一行,一个整数。
输入样例 :
5 3 1 5 4 2
输出样例 :
2
2、算法思路
这类题目需要在一个序列中不连续地找到子序列,让其满足一定的要求。在数据容量不大的情况下,可以使用全局变量+函数调用的方式进行遍历,具体实现方法如下面代码,在每一个函数中展开多个子函数直到达到终止条件。
3、代码实现
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
int max1=0;
int n;
int num[1000];
void fun(int i,int o){//函数输入:当前数列的最后一个数i,序列长度o
if(o>max1){
max1=o;
}//更新max1
for(int k=i+1;k<n;k++){//包含函数终止条件
if(num[k]>num[i])
fun(k,o+1);//若找到比i大的数,进入子函数
}
return;
}
int main(){
cin>>n;
for(int i=0;i<n;i++){
cin>>num[i];
}
for(int i=0;i<n;i++){
fun(i,1);
}
cout<<max1;
}
十三、兔子的公共祖先
1、问题描述
小红养了一些很可爱的兔子。 有一天,她突然发现兔子们都是严格按照伟大的数学家斐波那契提出的模型来进行繁衍:一对兔子从出生后第二个月起,每个月刚开始的时候都会产下一对小兔子。我们假定, 在整个过程中兔子不会出现任何意外。小红把兔子按出生顺序,把兔子们从1开始标号,并且小红的兔子都是 1 号兔子和 1 号兔子的后代。如果某两对兔子是同时出生的,那么小红会将父母标号更小的一对优先标号。
如果我们把这种关系用图画下来,前六个月大概就是这样的:
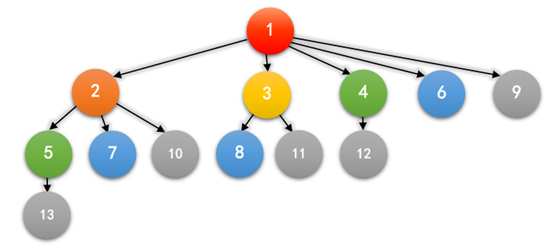
其中,一个箭头 A → B 表示 A 是 B 的祖先,相同的颜色表示同一个月出生的兔子。
为了更细致地了解兔子们是如何繁衍的,有一个问题:她想知道关于每两对兔子ai和bi,他们的最近公共祖先是谁。
一对兔子的祖先是这对兔子以及他们父母(如果有的话)的祖先,而最近公共祖先是指两对兔子所共有的祖先中,离他们的距离之和最近的一对兔子。比如,5 和 7 的最近公共祖先是 2,1 和 2 的最近公共祖先是 1,6 和 6 的最近公共祖先是 6。
输入格式:
一行包含 2 个正整数,表示a和b。
输出格式:
答案,一个正整数。
输入样例:
2 3
输出样例:
1
2、算法思路
首先观察其数学模型,我们可以看到每个月出生的兔子的对数满足斐波那契数列,从2号兔子开始算起,每一个月出生的兔子对数为:1、1、2、3、5、8……
而且,当月出生的兔子的祖先从1递增,如:6~8号兔子是同一个月出生的,它们的祖先依次为1、2、3;9~13号兔子是同一个月出生的,它们的祖先依次为1、2、3、4、5。
以此,我们可以构建一个数组rabbit[],用以存储每一只兔子的双亲,我们需要判断的即为rabbit[a]与rabbit[b]的共同祖先。
对于rabbit[a]与rabbit[b]的共同祖先,我们可以以如下方法判断:
- 当
rabbit[a]==rabbit[b],找到共同祖先。 - 当
rabbit[a]==b或rabbit[b]==a,找到共同祖先。 - 如果不满足上述两种情况,当
rabbit[a]<rabbit[b],则取b=rabbit[b],(更新较大的rabbit),并继续比较;反之也相同。
3、代码实现
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
int main(){
int a,b;
cin>>a>>b;
if(a==b){
cout<<a;
return 0;
}//特殊情况
int num[100],rab[1000];
num[0]=1;
num[1]=1;
int i=2;
while(i){
num[i]=num[i-1]+num[i-2];
if(num[i]>a && num[i]>b)break;
i++;
}//构造斐波那契数列
int x=0;
for(int j=0;j<i;j++){
for(int k=0;k<num[j];k++){
rab[x]=k+1;
x++;
}
}//构造rabbit数组
int A=a-2,B=b-2;
while(1){
if(rab[A]==rab[B]){
cout<<rab[A];
break;
}
else if(A==rab[B]-2){
cout<<A+2;
break;
}
else if(B==rab[A]-2){
cout<<B+2;
break;
}
else{
if(rab[A]<rab[B]){
B=rab[B];
}
else A=rab[A];
}
}//判断
}
十四、重复的DNA序列
1、问题描述
所有 DNA 都由一系列缩写为 A,C,G 和 T 的核苷酸组成,如:“ACGAATTCCG”。编写一个函数来查找 DNA 分子中所有出现超过一次的 10 个字母长的序列(子串)。
输入格式:
一行DNA序列。
输出格式:
所有重复的子串。
输入样例 :
AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT
输出样例 :
AAAAACCCCC CCCCCAAAAA
2、算法思路
最简单的算法为从头读取10位长的字符串,并将每个子串与该子串位置后面的字符串比较,将符合结果的字符串输出。
问题的另一个难点为输出顺序,测例中的输出顺序是根据字典排序的,所以我们需要将符合结果的字符串先存储起来,最后再根据字典排序输出。这里可以用set进行自动的排序。
3、代码实现
#include <iostream>
#include <string>
#include <set>
#include <string>
#include <algorithm>
using namespace std;
set<string> S;//容器
void com(string str,int i){
for(int k=i+1;k<str.size()-10;k++){
string t=str.substr(k,10);
string s=str.substr(i,10);
if(s==t){
S.insert(s);//满足条件,插入
return;
}
}
}
int main() {
string str;
cin>>str;
for(int i=0;i<str.size()-10;i++){
com(str,i);
}
for(set<string>::iterator it=S.begin();it!=S.end();it++)
cout<<*it<<endl;//迭代器遍历
}
十五、索引处的解码字符串
1、问题描述
给定一个编码字符串 S。为了找出解码字符串并将其写入磁带,从编码字符串中每次读取一个字符,并采取以下步骤:
如果所读的字符是字母,则将该字母写在磁带上。
如果所读的字符是数字(例如 d),则整个当前磁带总共会被重复写 d-1 次。
现在,对于给定的编码字符串 S 和索引 K,查找并返回解码字符串中的第 K 个字母。
输入格式:
两行,第一行为编码的字符串,第二行为K
输出格式:
解码后的第K个字母。
输入样例 :
leet2code3 10
输出样例 :
o
解释 :
解码后的字符串为 “leetleetcodeleetleetcodeleetleetcode”。 字符串中的第 10 个字母是 “o”。
2、算法思路
依次读取原字符串str的每一位,解码得出结果字符串code,将其输出即可。
将字符串中的连续数字转换为整型的框架如下:
int num=0;
if(str[i]<='9' && str[i] >= '0'){
num*=10;
num+=(str[i]-'0');
}
但是,检查测例中出现了一种特殊情况:a2445657646,且输出的为第1个字母。如果将此字符串解码,无疑会发生越界。那么,我们只能在解码时增加一点限制条件,让其不发生越界,且满足其他测例的解码要求。(我使用的方法是限制转换得到的数字的大小,让数字大小的上界不超过某一个较大的数,这样可以保证不发生越界,且满足其他测例)
3、代码实现
#include <iostream>
#include <string>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
int main() {
string str,code;
cin>>str;
int n;
cin>>n;
int num=0;
for(int i=0;i<=str.size();i++){
if(str[i]<='9' && str[i] >= '0'){
if(num>n*100){
break;
}//限制大小
num*=10;
num+=(str[i]-'0');
}
else {
if(num){
string code0=code;
for(int j=0;j<num-1;j++){
code+=code0;
}
num=0;
}
code+=str[i];
}
}
cout<<code[n-1];
}
十六、拼数
1、问题描述
设有n个正整数,将它们联接成一排,组成一个最大的多位整数。 输入格式 第一行,一个正整数n。 第二行,n个正整数。 输出格式 一个正整数,表示最大的整数
输入样例 :
3 13 312 343
输出样例 :
34331213