数据结构复习
第一章:引言
1.基本概念
数据:一切能输入到计算机中并能被计算机程序识别和处理符号的
数据类型:value+operations
数据元素(data element):数据的基本单位
data item:构成数据元素的最小单位
data object:具有相同形式的数据元素的集合
ADT :Abstract data Type 抽象数据类型
算法的五个重要特性:确定性,可行性,输入,输出,有限性
分析算法的四个方面:正确性,可读性,健壮性,效率(时间,空间)
第二章:线性结构
1.线性表
线性存储结构:
元素之间逻辑的相继关系用物理上的相邻关系来表示(逻辑上相邻的元素在物理位置上也相邻)
数组线性表数据插入
int insertelemm( list *L,int x,int i)
{
int j;
for(j=L.last;j>=i;j--)
{
L.data[j+1]=L.data[j];
}
L.data[i]=x;
L.last++;
}
优点:结构简单,存储效率高
缺点:插入,删除算法效率低,对长度大的小型吧,操作不方便
2.链表 Linkedlist
元素之间的逻辑相邻关系用指针来表示
插入方式
void insert(ListNode *head,int pos,int x)//在pos后插入
{
ListNode *p,*q;
p=head;
int i;
for(i=0;i<pos;i++)
{
p=p->next;
}
q=new ListNode(x);
q->next=p->next;
p->next=q;
}
优点:插入删除比较快,灵活
缺点:访问元素费时间
//链表的就地旋转
void convert(Linklist *la)
{
Linklist *p,*q;
p=la->next;
la->next=NULL;
while(p!=NULL)
{
p=q;
p=p->next;
q->next=la;
la=q;
}
}
3.栈结构 Stack
仅限在表尾进行插入和删除的线性表(后进先出)
Operation:
入栈:push 出栈 pop 得到头结点 top
递归实现全排列
#include <iostream>
using namespace std;
void swap(int &a,int &b){
int temp=a;
a=b;
b=temp;
}
void perm(int list[],int low,int high){
if(low==high){ //当low==high时,此时list就是其中一个排列,输出list
for(int i=0;i<=low;i++)
cout<<list[i];
cout<<endl;
}else{
for(int i=low;i<=high;i++){//每个元素与第一个元素交换
swap(list[i],list[low]); //将递归的第一个元素与后面的每个元素交换
perm(list,low+1,high); //交换后,得到子序列,用函数perm得到子序列的全排列 交换后继续执行实现后面的数的交换
swap(list[i],list[low]);//最后,将元素交换回来,复原,然后交换另一个元素 执行输出后,按从内到外交换回来,返回出来原函数。
}
}
}
int main()
{
int list[]={1,2,3};
perm(list,0,2);
return 0;
}
4.队列 Queue
只允许在一段进行插入操作,在另外一段进行删除操作的线性表(先进先出)
Operations:
initQueue()//初始化:
empty()//判断是否为空
pop()//出队
push()//入队
5.字符串 String
字符串匹配算法
next 求法人为看第j项前 最长相等前后缀
//nextval求法
for(i=1;i<max;i++)
{
if(T[j]==T[next[j]])
{
nextval[j]=nextval[next[j]];
}
else nextval[j]=next[j];
}
6.数组和广义表
特殊矩阵的压缩
1)对称矩阵

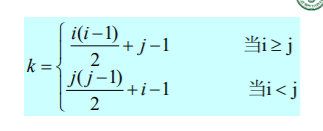
2)稀疏矩阵
三元法

三元法的转置
粗暴算法:

改进算法:
使用两个数组num,cpot
num记录m中每列元素个数,cpot通过num求出每一列元素开始位置
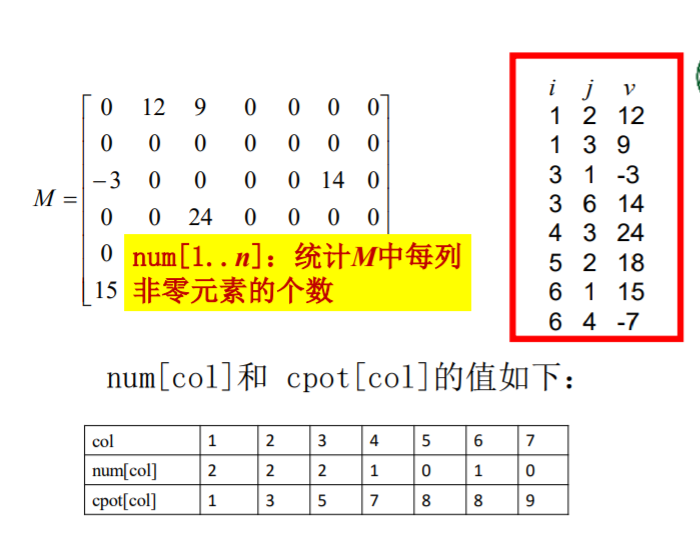
然后扫描放进去
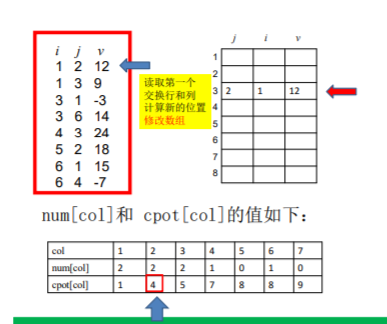
广义表定义
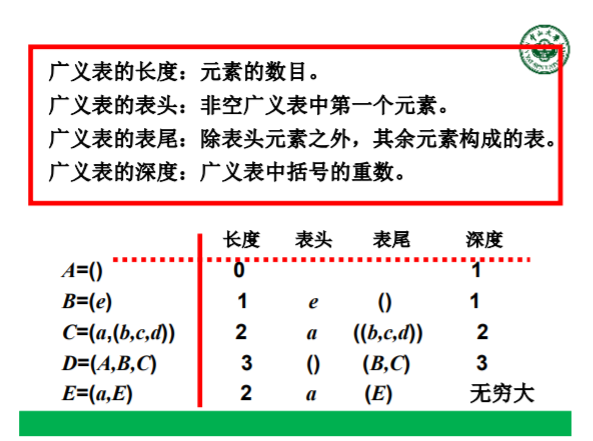
第三章:树
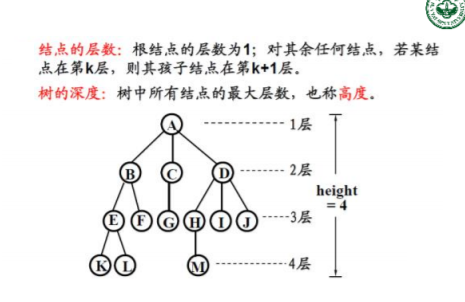
1.树的定义
结点的度:结点的子树
分支结点:度不为0的结点
叶:度为0的结点
子女结点:某结点子树的根节点
双亲结点:某个结点是其子树之根的双亲
兄弟结点:具有同一双亲的所有结点
2.存储设计
1)双亲表示法
每个结点有一个编号和存储信息,并存储他们的双亲的编号
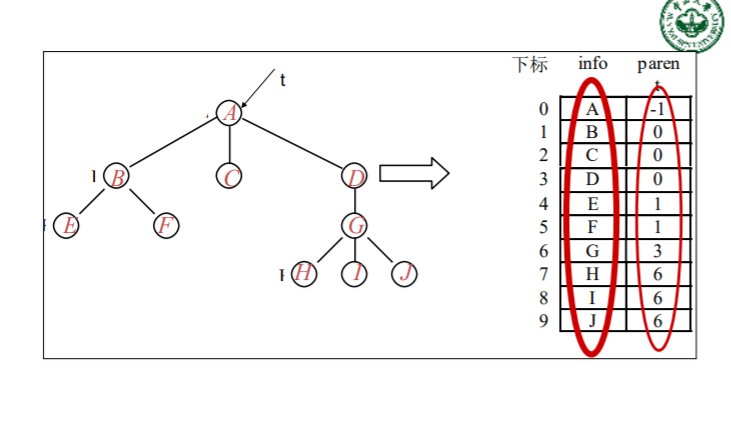
2)孩子表示法
孩子表示法主要描述的是结点与孩子的关 系。由于每个结点的孩子个数不定,所以利 用链式存储结构更加适宜。
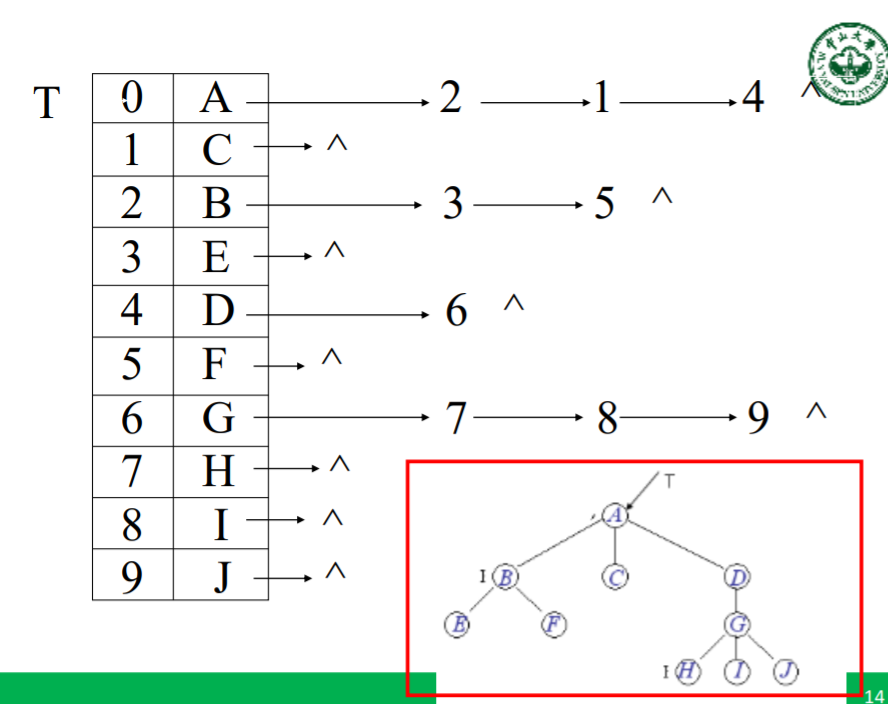
3)孩子兄弟表示法
孩子兄弟表示法也是一种链式存储结构。它通过描述每 个结点的一个孩子和兄弟信息来反映结点之间的层次关系, 其结点结构为:
其中,firstchild为指向该结点第一个孩子的指针, nextsibling为指向该结点的下一个兄弟,item是数据元素 内容。
3.二叉树
1) 若二叉树的层次从1开始, 则在二叉树 的第 i 层最多有 2^i-1^个结点。(i >=1)
2)高度为k的二叉树最多有 2 ^k^ -1个结点。
3)对任何一棵二叉树, 如果其叶结点个 数为n0 , 度为2的非叶结点个数为 n~2~, 则有 n~0~=n~2~+1
4)具有n个结点的完全二叉树的 高度为 (log~2~n)~up~ +1
5)
4.树与二叉树的相互转化
1)树转化为二叉树
将树转换成二叉树的步骤是:
1.加线。就是在所有兄弟结点之间加一条连线;
2.抹线。就是对树中的每个结点,只保留他与第一个孩子结点之间的连线,删除它与其它孩子结点之间的连线;
3.旋转。就是以树的根结点为轴心,将整棵树顺时针旋转一定角度,使之结构层次分明。

2)二叉树转化为树
1.若某结点的左孩子结点存在,将左孩子结点的右孩子结点、右孩子结点的右孩子结点……都作为该结点的孩子结点,将该结点与这些右孩子结点用线连接起来;
2.删除原二叉树中所有结点与其右孩子结点的连线;
3.整理(1)和(2)两步得到的树,使之结构层次分明。

5.二叉树的遍历
1)中序遍历
左子树->根节点->右子树
2)前序遍历
根节点->左子树->右子树
3)后序遍历
左子树->右子树->根节点
4)层序遍历
一层一层的遍历
void cengxu(Node *root){
queue<Node*> q;
Node *front;
if(root == NULL) return;
q.push(root);
while(!q.empty()){
front = q.front();
q.pop();
if(front->left) q.push(front->left);
if(front->right) q.push(front->right);
cout << front->key<< " ";
}
}
6.哈夫曼编码
#include<iostream>
#include<vector>
using namespace std;
struct Huff_Node
{
int weight;
char str;
string code;
int left;
int right;
int parent;
};
int main()
{
int n;
cin>>n;
int a;
char b;
vector<int> num;
vector<char> ss;
int i,j,k;
for(i=0;i<n;i++)
{
cin>>a;
cin>>b;
num.push_back(a);
ss.push_back(b);
}
vector<int> weight;
for(i=0;i<n-1;i++)
{
for(j=i+1;j<n;j++)
{
if(num[j]>num[i])
{
b=ss[i];
ss[i]=ss[j];
ss[j]=b;
a=num[i];
num[i]=num[j];
num[j]=a;
}
}
}
for(i=0;i<n;i++)
{
weight.push_back(num[i]);
}
Huff_Node *huff = new Huff_Node[n * 2 - 1];
for(i=0;i<2*n-1;i++)
{
huff[i].left=-1;
huff[i].right=-1;
huff[i].parent=-1;
huff[i].code="";
if(i<n)
{
huff[i].str=ss[i];
huff[i].weight=num[i];
}
}
int min1,min2,left,right;
for(j=n;j<2*n-1;j++)
{
min1=1000;
min2=1000;
left=-1;
right=-1;
for(k=0;k<j;k++)
{
if(huff[k].parent==-1)
{
if(huff[k].weight < min1)
{
min2 = min1;
min1 = huff[k].weight;
right = left;
left = k;
}
else if(huff[k].weight < min2)
{
min2=huff[k].weight;
right=k;
}
}
}
huff[j].weight = huff[left].weight + huff[right].weight;
huff[j].left = left;
huff[j].right = right;
huff[left].parent = j;
huff[right].parent = j;
}
for (int i = 0; i < n; i++)
{
string code = "";
int j = i;
while (huff[j].parent != -1)
{
int k = huff[j].parent;
if (huff[k].left==j)
{
code = "0" + code;
}
else
{
code = "1" + code;
}
j = k;
}
huff[i].code = code;
}
for(i=0;i<n;i++)
{
cout<<huff[i].weight<<huff[i].code<<endl;
}
}
第四章 图
1.基本概念
1)一个顶点v的度是与它相关联的边的条数;
2)顶点的出度: 以顶点v为弧尾的弧的数目;
3)顶点的入度: 以顶点v为弧头的弧的数目。
4)顶点的连通性:在无向图中, 若从顶点vi到顶点vj (i≠j)有路径, 则称顶点vi与vj是连通的。
5)连通图:如果一个无向图中任意一对顶点都是连通的, 则称 此图是连通图。
6) 连通分量:非连通图的极大连通子图叫做连通分量。
7)强连通性:在有向图中, 若对于每一对顶点vi和vj ( i≠j), 都存在一条从vi到vj和从vj到vi的有向路径,则称顶点vi与 vj是强连通的。
8)强连通图:如果一个有向图中任意一对顶点都是强连通的, 则 称此有向图是强连通图。
2.图的表示
1)邻接矩阵
typedef struct{
vertextype v[n];
int juzhen[n][n];
int vexnum,arcnum;
}MGraph;

2)邻接表
class EdgeNode {
public:
int adjvex; //边指向哪个顶点的索引
int weight;
EdgeNode* next;
};
// 顶点表结构
class VertexNode {
public:
int value; //顶点的值,为了简化与序号相同,第一个是0
EdgeNode *firstedge;
};
// 图结构
class GraphList {
public:
VertexNode adjList[MAXVEX];
int numVertex;
int numEdges;
};
void createGraph(GraphList* g)
{
int k,m;
EdgeNode *t;
cin>>k;
cin>>m;
int p,q,num;
int i;
g->numEdges=m;
g->numVertex=k;
for(i=0;i<k;i++)
{
cin>>g->adjList[i].value;
}
for(i=0;i<m;i++)
{
cin>>p>>q>>num;
if(g->adjList[p].firstedge==NULL)
{
g->adjList[p].firstedge=new EdgeNode;
g->adjList[p].firstedge->adjvex=q;
g->adjList[p].firstedge->weight=num;
}
else
{
t=g->adjList[p].firstedge;
while(t->next!=NULL)
{
t=t->next;
}
t->next=new EdgeNode;
t->next->adjvex=q;
t->next->weight=num;
}
}
}
3.图的遍历
1)DFS深度优先搜索
(1)从图中的某个顶点v出发,访问之;
(2)依次从顶点v的未被访问过的邻接点出 发,深度优先遍历图,直到图中所有和顶 点v有路径相通的顶点都被访问到;
(3)若此时图中尚有顶点未被访问到,则另选 一个未被访问过的顶点作起始点,重复上述(1)(2)的操作,直到图中所有的顶 点都被访问到为止。
void DFS(GraphList *g,int v,int *visit)
{
cout<<g->adjList[v].value<<" ";
visit[v]=1;
EdgeNode *e;
e=g->adjList[v].firstedge;
while(e!=NULL)
{
if(visit[e->adjvex]==0)
DFS(g,e->adjvex,visit);
e=e->next;
}
}
void DFSTraverse(GraphList *g)
{
int *visit=new int [g->numVertex];
int i;
for(i=0;i<g->numVertex;i++)
{
visit[i]=0;
}
for(i=0;i<g->numVertex;i++)
{
if(visit[i]==0)
{
DFS(g,i,visit);
}
}
}
2)BFS广度优先搜索
(1)从图中的某个顶点v出发,访问之;
(2)依次访问顶点v的各个未被访问过的邻接点,将v的全部邻接点都访问到;
(3)分别从这些邻接点出发,依次访问它们的 未被访问过的邻接点,并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接 点”被访问,直到图中所有已被访问过的顶 点的邻接点都被访问到。
void BFS(GraphList *g,int v,int *visit)
{
cout<<g->adjList[v].value<<" ";
visit[v]=1;
queue<int> q;
q.push(v);
while(!q.empty())
{
int w=q.front();
q.pop();
EdgeNode *e;
e=g->adjList[w].firstedge;
while(e!=NULL)
{
if(visit[e->adjvex]==0)
{
cout<<e->adjvex<<" ";
visit[e->adjvex]=1;
q.push(e->adjvex);
}
e=e->next;
}
}
}
void BFSTraverse(GraphList *g)
{
int *visit=new int [g->numVertex];
int i;
for(i=0;i<g->numVertex;i++)
{
visit[i]=0;
}
for(i=0;i<g->numVertex;i++)
{
if(visit[i]==0)
{
BFS(g,i,visit);
}
}
}
4.最小生成树
1)Prim算法
(1)在连通网的顶点集合V中,任选一个顶点, 构成最小生成树的初始顶点集合U;
(2)在U和V-U中各选一个顶点,使得该边的权值最小,把该边加入到最小生成树的边集TE中, 同时将V-U中的该顶点并入到U中;
(3)反复执行第(2)步,直至V-U=Ø为止。
引入一个辅助数组记录现有顶点到各顶点的最小权值
| 顶点 | 0 | 1 | 2 | 3 | 4 | 5… |
|---|---|---|---|---|---|---|
| lowcost | ||||||
| adjvex |
void Prim(Graph G,MST & T,int u)
{
float *lowcost=new float[vernum];
int *adjvex=new int [vernum];
for(int i=0;i<vernum;i++)
{
lowcost[i]=G.edge[u][i];
adjvex[i]=u;
}
adjvex[u]=-1;
int k=0;
for(i=0;i<G.n;i++)
{
if(i!=u)
{
min=10000;
int v=0;
for(j=0;j<vernum;j++)
{
if(adjvex[j]!=-1&&lowcost[j]<min)
{
v=j;
min=lowcost[j];
}
}
}
if(v)
{
T[k].tail=adjvex[v];
T[k].head=v;
T[k++].cost=lowcost[v];
adjvex[j]=-1;
for(j=0;j<G.n;j++)
{
if(adjvex!=-1&&G.edge[v][j]<lowcost[j])
{
lowcost[j]=G.edge[v][j];
adjvex[j]=v;
}
}
}
}
}
2)Kruskal算法
基本思想:
设有一个有 n 个顶点的连通网络 N = { V, E },最初先 构造一个只有 n 个顶点,没有边的非连通图 T = { V, }, 图中每个顶点自成一个连通分量。当在 E 中选到 一条具有最小权值的边时,若该边的两个顶点落在不同 的连通分量上,则将此边加入到 T 中;否则将此边舍 去,重新选择一条权值最小的边。如此重复下去,直 到所有顶点在同一个连通分量上为止。
5. AOV网
用顶点表示活动,用有向边表示活动间 的优先关系。v~i~ 必须先于活动v~j~进行。这种有 向图叫做顶点表示活动的AOV网络(Activity On Vertices)。
1)拓扑排序
① 输入AOV网络。令 n 为顶点个数。
② 在AOV网络中选一个没有直接前驱的顶点, 并输出之;
③ 从图中删去该顶点, 同时删去所有它发出 的有向边;
④ 重复以上 ②、③步, 直到
全部顶点均已输出,拓扑有序序列形成, 拓扑排序完成;
图中还有未输出的顶点, 但已跳出处理 循环。说明图中还剩下一些顶点, 它们都有直接前驱。这时网络中必存在有向环。
void Graphcircle(GraphList *g){
int count[g->numVertex],del[g->numVertex];
for(int i=0;i<g->numVertex;i++){
del[i]=0;
count[i]=0;
}
for(int i=0;i<g->numVertex;i++){
EdgeNode *p=g->adjList[i].firstedge;
while(p){
count[p->adjvex]++;
p=p->next;
}
}//初始化count
stack<int> sta;
int num=0;
for(int i=0;i<g->numVertex;i++){
if(count[i]==0){
sta.push(i);
}
}//第一个入栈
while(!sta.empty()){
int w=sta.top();
sta.pop();
//cout<<w<<endl;
num++;
del[w]=1;//记录该点是否被删除
EdgeNode *p=g->adjList[w].firstedge;
while(p){
count[p->adjvex]--;
if(count[p->adjvex]==0){
sta.push(p->adjvex);
}
p=p->next;
}
for(int i=0;i<g->numVertex;i++){
if(count[i]==0 && del[i]==0)
{
sta.push(i);
}
}
}
}
5)AOE网络
从源点到各个顶点,以至从源点到汇点的有向路径可 能不止一条。这些路径的长度也可能不同。完成不同 路径的活动所需的时间虽然不同,但只有各条路径上 所有活动都完成了,整个工程才算完成。
因此,完成整个工程所需的时间取决于从源点到汇点 的最长路径长度,即在这条路径上所有活动的持续时 间之和。这条路径长度最长的路径就叫做关键路径 (Critical Path)。





int *etv,*ltv;
int *stack2;
int top2;
Status TopologicalSort(GraphAdjList GL)
{
EdgeNode *e;
int i,k,gettop;
int top=0;
int count=0;
int *stack;
stack=new int(GL -> vernum);
for(i=0;i<GL->vernum;i++)
{
if(GL->adjList[i].in==0)
{
stack[++top]=i;
}
}
evt=new int(GL -> vernum);
for(i=0;i<GL->vernum;i++)
{
evt[i]=0;
}
stack=new int(GL->vernum);
while(top!=0)
{
gettop=stack(top--);
count++;
stack2[++top2]=gettop;
for(e=GL->adjList[gettop].firstedge;e;e=e->next)
{
k=e->adjvex;
GL->adjList[k].in--;
if(GL->adjList[k]==0)
{
stack[++top]=k;
}
if(etv[gettop]+e->weight>etv[k])
{
etv[k]=etv[gettop]+e->weight;
}
}
}
}
void CriticalPath(GraphAdjList GL)
{while
EdgeNode *e;
int i,gettop,k,j;
int ete,lte;
TopologicalSort(GL);
ltv=new int (GL->vernum);
for(i=0;i<GL->vernum;i++)
{
ltv[i]=etv[GL->vernum-1];
}
while(top2!=0)
{
gettop=stack2[top2--];
for(e=GL->adjList[gettop];e;e=e->next)
{
k=e->adjvex;
if(ltv[k]-e->weight<ltv[gettop])
{
ltv[gettop]=ltv[k]-e->weight;
}
}
}
for(j=0;j<GL->vernum;j++)
{
for(e=GL->adjList[j].firstedge;e;e=e->next)
{
k=e->adjvex;
ete=etv[j];
lte=ltv[k]-e->weight;
if(ete==lte)
{
cout<<GL->adjList[j].data<<GL->adjList[k].data<<e->weight;
}
}
}
}
6.最短路径
1)Dijkstra算法
① 初始化: S ← { v0 }; dist[j] ← Edge[0] [j], j = 1, 2, …, n-1; // n为图中顶点个数
② 求出最短路径的长度: dist[k] ← min { dist[i] }, i V- S ; S ← S U { k };
③ 修改: dist[i] ← min{ dist[i], dist[k] + Edge [k] [i] }, 对于每一个 i V- S ;
④ 判断:若 S = V, 则算法结束,否则转 ②。
void ShortestPath(MTGraph G,int v)
{
EdgeData dist[G.num];
int path[G.num];//记录该点的上一个顶点
int S[G.num];//记录是否已经放进路径当中
for(int i=0;i<G.num;i++)
{
dist[i]=G.Edge[v][i];
S[i]=0;
if(i!=v&&dist[i]<max)
{
path[i]=v;
}
else path[i]=-1;
}
S[v]=1;dist[v]=0;
for(int i=0;i<G.num-1;i++)
{
int min=10000;
for(int j=0;j<G.num;j++)
{
if(!S[j]&&dist[j]<min)
{
min=dist[j];
u=j;
}
}
S[u]=1;
for(int k=0;k<G.num;k++)
{
if(!S[k]&&G.edge[u][k]<max&&G.edge[u][k]+dist[u]<dist[k])
{
dist[k]=G.edge[u][k]+dist[u];
path[k]=u;
}
}
}
for(int i=0;i<G.num;i++)
{
//路径输出
}
}
2)所有顶点之间的最短路径



代码:
#include<iostream>
#include <vector>
using namespace std;
const int inf = 999999;
const int n = 6;
int L[n][n] = { 0, 7, 9,inf,inf, 14,
7, 0, 10, 15,inf,inf,
9, 10, 0, 11,inf, 2,
inf, 15, 11, 0, 6,inf,
inf,inf,inf, 6, 0, 9,
14, inf, 2,inf, 9, 0
}; //存储图中的路径
int dis[n][n]; //存储源点到各个顶点的最短路径
vector<int> path[n];
int main()
{
for (int i = 0; i < n; i++) //初始化
{
for (int j = 0; j < n; j++)
{
dis[i][j] = L[i][j];
path[i][j].push_back(i+1);
path[i][j].push_back(j+1);
}
}
for (int k = 0; k < n; k++)
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
//dis[i] = min(dis[i],dis[j] + L[j][i]);
if (dis[k][i] > dis[k][j] + L[j][i]) //求源点到节点的最短路径,利用现有的L矩阵
{
dis[k][i] = dis[k][j] + L[j][i];
path[k][i].clear(); //保存并更新路径
path[k][i].insert(path[k][i].end(), path[k][j].begin(),path[k][j].end());
path[k][i].push_back(i+1);
}
}
}
}
vector<int>::iterator ite;
for (int k = 0; k < n; k++)
{
for (int i = 0; i < n; i++)
{
cout << "源点"<<k+1<<"到"<<i+1<<"的最短路径长度:" << dis[k][i]<<endl<<"Path:";
for (ite = path[k][i].begin(); ite !=path[k][i].end();++ite) {
if (ite == path[k][i].begin())
cout << *ite;
else
cout << "->"<< *ite ;
}
cout << endl;
}
}
return 0;
}
7.网络流



如果一个节点被移去是,图被分成两个或多个部分,则称该节点为关节点
没有关节点的连通图为双连通图
第五章 查找
1.基本概念
查找:就是在数据集合中寻找满足某种条 件的数据对象。
查找表:是由同一类型的数据元素(或记录) 组成的数据集合。
关键字:数据元素中某个数据项的值, 用以标识一个数据元素。
主关键字:可唯一地标识一个数据元素的关键字。
次关键字:用以识别若干记录的关键字。
2.查找方法
1)顺序查找
查找过程:从表中最后一个元素开始,顺序用各元 素的关键字与给定值x进行比较,若找到与其值相等 的元素,则查找成功,给出该元素在表中的位置; 否则,若直到第一个记录仍未找到关键字与x相等的 对象,则查找失败。
for(i=n;i>0;i--)
{
if(a[i]==p)
return i;
}
顺序查找 时间复杂性O(n)
插入、删除的时间复杂性O(1)
2)折半查找
前提条件:表中的关键字有序
⑴ 取中间位置Mid:Mid=(Low+High)/2 ;
⑵ 比较中间位置记录的关键字与给定的K值:
① 相等: 查找成功;
② 大于:待查记录在区间的前半段,修改上界指 针: High=Mid-1,转⑴ ;
③ 小于:待查记录在区间的后半段,修改下界指 针:Low=Mid+1,转⑴ ;直到越界(Low>High),查找失败。
int Bin_search(STable ST,int key)
{
int low=0,high=ST.lenth-1,mid;
while(low<high)
{
mid=(low+high)/2;
if(key==ST[mid])
{
return mid;
}
else if(key<ST[mid])
{
high=mid-1;
}
else
low=mid+1;
}
return 0;
}
折半查找的时间负责性为O(log n)
插入、删除的时间复杂性为O(n)
3)分块查找
分块查找:又称索引顺序查找,是 前面两种查找方法的综合。
① 将查找表分成几块。块间有序,即第i+1块的所有记录关 键字均大于(或小于)第i块记录关键字;块内无序。
② 在查找表的基础上附加一个索引表,索引表是按关键字有 序的。int Block_search(int *ST,index *ind,int key,int n,int b)//n为表长,b为块数
{
int i=0,j,k;
while(i<b)
{
if(ind[i].maxkey>key)
i++;
}
if(i>b){cout<<"not found";return 0;}
j=ind[i].starypos;
while(j<n)
{
if(ST[j].key==key)
{
break;
}
j++;
}
if(j>n||ST[j].key!=key)
{
cout<<"no found";
retuen 0;
}
return j;
}
4)优先队列
给定一个具有m个关键字的序列,如果在该序列 中,满足: 对 i= m/2→ 1的元素,k~i~<=k~2i~且k~i~<=k~2i+1~,则该序列称为优先队列(堆)


构建代码:
void HeapAdjust(HeapType &H ,int s,int m)
{//最大堆的向下调整算法
int rc=H.r[s];
for(int j=2*s;j<m;j*=2)
{
if((j<m)&&(H.r[j].key<H.r[j+1].key))
{
j++;
}
if(rc.key>H.r[j].key)break;
H.rs[s].key=H.rs[k].key;s=j
}
H.r[s]=rc;
}
插入O(log n)
查找删除O(1)
5)哈希表
散列技术的基本思想:
把元素的存储位置和该记录的关键字的值之间建立一个映射关系。关键字的值在这种映射关系下的像,就是相应记录在表中的存储位置。
相关概念:
散列:将记录按照其关键字的散列地址存储到散列表中的过程
散列冲突:不同关键字具有相同的散列地址
相关构造方法:
1.直接定址法(线性函数)
2.数字分析法

3.平方取中法

4.折叠法

5.除留余数法
设散列表中允许的地址数为m,取一个不大于m,但最接近于或 等于m的质数p,或选取一个不小于20的质因数的合数作为除数, 利用以下公式把关键字转换成散列地址。散列函数为:
$hash ( key ) = key $%p ,$ p <= m$

6.散列技术
1)线性探测法


2)二次探测法

3)再哈希法

3)链地址法


4)哈希查找


第六章 排序
1.基本概念
排序:将一组杂乱无章的数据排列成一个按关键字有序的序列
数据表:它是特定排序数据对象的有限集合
关键字:通常数据对象有多个属性域,即多个数据成员组成,其 中有一个属性域可用来区分对象,作为排序依据。该域即为关键字。每 个数据表用哪个属性域作为关键字,要视具体的应用需要而定。即使是 同一个表,在解决不同问题的场合也可能取不同的域做关键字。
2.排序方法
1)插入排序
每步将一个待排序的对象,按其关键字大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入为止。

void InsertSort(int *a)
{
int i,j,temp=0;
for(i=1;i<n;i++)
{
temp=a[i];
j=i-1;
for(;j>=0&&a[j]>temp;j--)
{
a[j+1]=a[j];
}
a[j+1]=temp;
}
}
算法分析:
最好情况为本来有序O(n)
稳定为O(n^2^)
2)希尔排序
基本思想:
先将整个待排对象序列按照一定间隔分割成为若干子序列,分别进行直接插入排序,然后缩小间隔,对整个对象序列重复以上的划分子序列和分别排序工作,直到最后间隔为1,此时整个对象序列已 “基本有序”,进行最后一次直接插入排序。
void shellsort(int *a)
{
int d=n;
while(d!=1)
{
d/=2;
for(int x=0;x<d;x++)
{
for(int i=x+d;i<n;i+=d)
{
int temp=a[i];
int j;
for(j=i-d;j>=0&&a[j]>temp;j-=d)
{
a[j+d]=a[j];
}
a[j+d]=temp;
}
}
}
}
Knuth利用大量的实验统计资料得 出,当n很大时,关键字平均比较 次数和对象平均移动次数大约在 n ^1.25^ 到 1.6*n^1.25^ 的范围内。这是在利 用直接插入排序作为子序列排序方 法的情况下得到的。
3)冒泡排序
void bubblesort(int *a)
{
int i,j;
bool change=1;
for(i=n-1;i>0&&change==1;i--)
{
change=0;
for(j=0;j<i;j++)
{
if(a[j+1]<a[j])
{
int temp=a[j+1];
a[j+1]=a[j];
a[j]=temp;
change=1;
}
}
}
}
算法特点:
至少比较一次,至多比较n-1次,可实现部分排序,稳定排序
最理想O(n) 最坏情况O(n^2^)
4)快速排序
int getmid(int *a,int low,int high)
{
int temp=a[low];
while(low<high)
{
while(low<high&&a[high]>=temp)
{
high--;
}
a[low]=a[high];
while(low<high&&a[low]<=temp)
{
low++;
}
a[high]=a[low];
}
a[low]=temp;
return low;
}
void quicksort(int *a,int low,int high)
{
if(low<high)
{
int mid=getmid(a,low,high);
quicksort(a,low,mid-1);
quicksort(a,mid+1,high);
}
}
分析:
快速排序是一种不稳定的排序方法
对于n比较大的时候,速度快,但对于n比较小的时候,比其他排序慢
5)选择排序
void selectsort(int *a)
{
int i,j;
for(i=0;i<n;i++)
{
for(j=i+1;j<n;j++)
{
if(a[i]>a[j])
{
int temp=a[i];
a[i]=a[j];
a[j]=temp;
}
}
}
}
分析:
直接选择排序是一种不稳定的排序方法
时间复杂度为O(n^2^)
6)堆排序
参考上述优先队列
7)归并排序
void Merge(int *a,int l,int mid,int r)
{
int *temp=new int[r-l+1];
int i=0;
int p1=l;
int p2=mid+1;
while(p1<=mid&&p2<=r)
{
temp[i++]=a[p1]<a[p2]?a[p1++]:a[p2++];
}
while(p1<=mid)
{
temp[i++]=a[p1++];
}
while(p2<=r)
{
temp[i++]=a[p2++];
}
for(i=0;i<r-l+1;i++)
{
a[l+i]=temp[i];
}
}
void Msort(int *a,int l,int r)
{
if(l==r)return;
int mid=l+(r-l)/2;
Msort(a,l,mid);
Msort(a,mid+1,r);
Merge(a,l,mid,r);
}
void mergesort(int *a)
{
Msort(a,0,n-1);
}
8)基数排序
实现多关键字排序有两种常用的方法
最高位优先
最低位优先



若关键字有d位,则需要进行d次分配手机
基数排序是稳定的排序方法
各种排序的比较:
